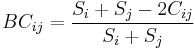Bray–Curtis dissimilarity

In ecology and biology, the Bray–Curtis dissimilarity, named after J. Roger Bray and John T. Curtis,^[1] is a statistic used to quantify the compositional dissimilarity between two different sites. It is equivalent to the total number of species that are unique to any one of the two sites divided by the total number of species over the two sites. In other words, it is the ratio between the turnover of species between the two sites and the total species richness over the two sites.

The short hand formula for the Bray–Curtis dissimilarity is:

$BC_{ij} = \frac{S_i %2B S_j - 2C_{ij}}{S_i %2B S_j}$

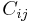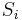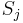Where $C_{ij}$ is the sum of minimum abundances of the various species (abundance at the site where the species is the rarest). $S_i$ and $S_j$ are the total number of specimens captured at both sites.^[2]

The Bray–Curtis dissimilarity is directly related to the Sørensen similarity index 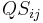$QS_{ij}$ between the same sites:

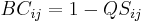$BC_{ij} = 1 - QS_{ij}$ .

The Bray–Curtis dissimilarity is bound between 0 and 1, where 0 means the two sites have the same composition (that is they share all the species), and 1 means the two sites do not share any species.

The Bray–Curtis dissimilarity is often erroneously called a distance. The Bray–Curtis dissimilarity is not a distance since it does not satisfy triangle inequality, and should always be called a dissimilarity to avoid confusion.

References

^ Bray, J. R. and J. T. Curtis. 1957. An ordination of upland forest communities of southern Wisconsin. Ecological Monographs 27:325-349.
^ Pierre Legendre & Louis Legendre. 1998. Numerical ecology. 2nd English edition. Elsevier Science BV, Amsterdam.